java之父高斯林

高斯消元算法是一个经典的数学算法，在计算机科学领域中也有广泛应用。在Java编程中，我们同样可以使用高斯消元算法来解决线性方程组问题。本文将为大家介绍一些实现高斯消元算法的基本思路和注意事项。

一、高斯消元算法基本实现步骤

高斯消元算法主要分为三个步骤：化简矩阵、回代和解方程。下面我们将一一介绍这些步骤的具体实现方法。

1. 化简矩阵

化简矩阵的目的是将线性方程组的系数矩阵转化为一个上三角矩阵。我们可以使用行变换的方法实现化简矩阵的过程。

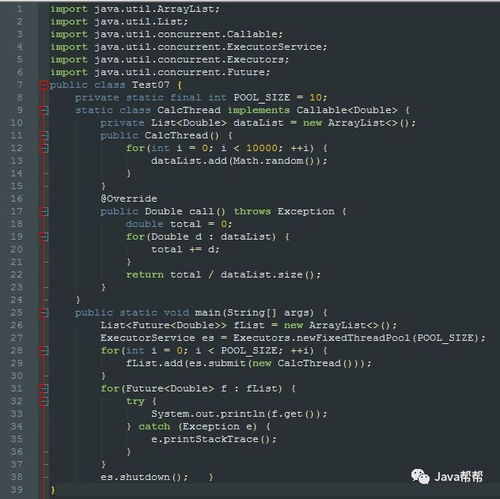
例如，对于以下的线性方程组：

$$

\begin{cases}

3x_1 2x_2 x_3= 1 \\

2x_1 2x_2 4x_3 = 2 \\

x_1 \frac{1}{2}x_2 x_3 = 0

\end{cases}

$$

系数矩阵为：

$$

\begin{bmatrix}

3 & 2 & 1\\

2 & 2 & 4\\

1 & \frac{1}{2} & 1

\end{bmatrix}

$$

我们需要将其化为上三角矩阵。我们将第一行乘以一个系数 $k$，然后减去第二行得到一个新的第二行：

$$

\begin{bmatrix}

3 & 2 & 1\\

0 & \frac{8}{3} & \frac{10}{3}\\

1 & \frac{1}{2} & 1

\end{bmatrix}

$$

接着，我们将第一行再乘以一个系数 $k'$，然后减去第三行得到一个新的第三行：

$$

\begin{bmatrix}

3 & 2 & 1\\

0 & \frac{8}{3} & \frac{10}{3}\\

0 & \frac{7}{3} & \frac{2}{3}

\end{bmatrix}

$$

这样，我们就得到了一个上三角矩阵。不过，需要注意的是：在进行行变换的时候，需要确保主元（系数矩阵的对角线元素）不为0。如果某一行的主元为0，则需要进行行交换操作，把一个非0元素移到主元的位置上。

2. 回代

回代的目的是将上三角矩阵转化为一个对角矩阵，使得每行只有一个未知数。我们可以从最后一行开始向上回代，逐个求解未知数的值。

例如，对于上述的上三角矩阵：

$$

\begin{bmatrix}

3 & 2 & 1\\

0 & \frac{8}{3} & \frac{10}{3}\\

0 & \frac{7}{3} & \frac{2}{3}

\end{bmatrix}

$$

我们可以从最后一行开始向上回代。最后一行的方程式为：

$$

\frac{7}{3}x_2 \frac{2}{3}x_3 = 0

$$

解出 $x_3$ 的值：

$$

x_3 = \frac{7}{2}x_2

$$

接着，将 $x_3$ 的值带入到第二行的方程式中：

$$

\frac{8}{3}x_2 \frac{10}{3}x_3 = 0

$$

解出 $x_2$ 的值：

$$

x_2 = \frac{5}{4}

$$

最终，将 $x_2$ 和 $x_

本文 新鼎系統网 原创，转载保留链接！网址：https://acs-product.com/post/17697.html